Produit vectoriel

Définition et Propriétés

\( \textbf{Définition}\):

On considère les vecteurs \(\vec{a}\) et \(\vec{b}\) relativement à une base orthonormée :

$$
\vec{a}=\left(\begin{array}{l}
a_{1} \\
a_{2} \\
a_{3}
\end{array}\right) \text { et } \vec{b}=\left(\begin{array}{l}
b_{1} \\
b_{2} \\
b_{3}
\end{array}\right)
$$

On appelle produit vectoriel des vecteurs \(\vec{a}\) et \(\vec{b}\), noté \(\vec{a} \times \vec{b}\), le vecteur défini par :

$$
\vec{a} \times \vec{b}=\left(\begin{array}{r}
a_{2} b_{3}-a_{3} b_{2} \\
-a_{1} b_{3}+a_{3} b_{1} \\
a_{1} b_{2}-a_{2} b_{1}
\end{array}\right)
$$

\( \textbf{Propriété géométrique:}\)

Soit \(\vec{a}\) et \(\vec{b}\) des vecteurs de \(V_{3}\).

Le vecteur \(\vec{a} \times \vec{b}\) est orthogonal à \(\vec{a}\) et \(\vec{b}\).

Preuve: Montrons que \((\vec{a} \times \vec{b}) \cdot \vec{a}=0\) et \((\vec{a} \times \vec{b}) \cdot \vec{b}=0\)

$$
\begin{aligned}
& (\vec{a} \times \vec{b}) \cdot \vec{a}=\left(\begin{array}{c}
a_{2} b_{3}-a_{3} b_{2} \\
-a_{1} b_{3}+a_{3} b_{1} \\
a_{1} b_{2}-a_{2} b_{1}
\end{array}\right) \cdot\left(\begin{array}{c}
a_{1} \\
a_{2} \\
a_{3}
\end{array}\right) \\
& =a_{2} b_{3} a_{1}-a_{3} b_{2} a_{1}-a_{1} b_{3} a_{2}+a_{3} b_{1} a_{2}+a_{1} b_{2} a_{3}-a_{2} b_{1} a_{3}=0 .
\end{aligned}
$$

De manière similaire, on a que \((\vec{a} \times \vec{b}) \cdot \vec{b}=0\).

\(\textbf{ Propriétés algébriques: }\)

\(\cdot \vec{a} \times \vec{b}=-(\vec{b} \times \vec{a})\)

– \((k \vec{a}) \times \vec{b}=k(\vec{a} \times \vec{b})=\vec{a} \times(k \vec{b})\)

– \(\vec{a} \times(\vec{b}+\vec{c})=\vec{a} \times \vec{b}+\vec{a} \times \vec{c}\)

– \((\vec{a}+\vec{b}) \times \vec{c}=\vec{a} \times \vec{c}+\vec{b} \times \vec{c}\)

– \(\vec{a} \times \vec{a}=\overrightarrow{0}\)

Sens de \(\vec{a} \times \vec{b}\) :

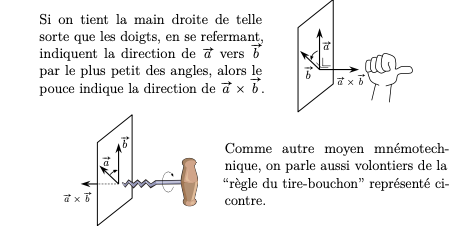
Le produit vectoriel des vecteurs \(\vec{a}\) et \(\vec{b}\) est un vecteur perpendiculaire au plan formé par \(\vec{a}\) et \(\vec{b}\) et dont le sens est donné par la “règle de la main droite” :

Si on tient la main droite de telle sorte que les doigts, en se refermant, indiquent la direction de \(\vec{a}\) vers \(\vec{b}\) par le plus petit des angles, alors \(\underset{\vec{b}}{\vec{l}}\) pouce indique la direction de \(\vec{a} \times \vec{b}\).

Définition

Propriétés

Applications

L’égalité suivante fournit un lien entre le produit vectoriel et le produit scalaire :

Identité de Lagrange: \(\|\vec{a} \times \vec{b}\|^{2}=\|\vec{a}\|^{2} \cdot\|\vec{b}\|^{2}-(\vec{a} \cdot \vec{b})^{2}\)

Calcul d’angles

\( \textbf{Proposition}\):

Soit \(\vec{a}\) et \(\vec{b}\) des vecteurs de l’espace, on a :

$$
\|\vec{a} \times \vec{b}\|=\|\vec{a}\| \cdot\|\vec{b}\| \cdot \sin (\theta)
$$

où \(\theta \in\left[0^{\circ} ; 180^{\circ}\right]\) est l’angle géométrique entre les vecteurs \(\vec{a}\) et \(\vec{b}\)

Preuve: Par l’identité de Lagrange, on a :

$$
\begin{aligned}
\|\vec{a} \times \vec{b}\|^{2} & =\|\vec{a}\|^{2} \cdot\|\vec{b}\|^{2}-(\vec{a} \cdot \vec{b})^{2} \\
& =\|\vec{a}\|^{2} \cdot\|\vec{b}\|^{2}-\|\vec{a}\|^{2} \cdot\|\vec{b}\|^{2} \cdot \cos ^{2}(\theta) \\
& =\|\vec{a}\|^{2} \cdot\|\vec{b}\|^{2} \cdot\left(1-\cos ^{2}(\theta)\right) \\
& =\|\vec{a}\|^{2} \cdot\|\vec{b}\|^{2} \cdot \sin ^{2}(\theta)
\end{aligned}
$$

En prenant la racine carrée de cette expression, on obtient le résultat qu’il fallait démontrer.

Remarque:

Le produit vectoriel est un outil que l’on utilise également en physique. Il permet, par exemple, de décrire le moment d’une force, ou la force sur une particule chargée en mouvement dans un champ magnétique. Notons alors que les physiciens le définissent par :

Le produit vectoriel de deux vecteurs \(\vec{a}\) et \(\vec{b}\) est un vecteur \(\vec{c}\). On écrit ce produit \(\vec{c}=\vec{a} \wedge \vec{b}\)

– La grandeur de \(\vec{c}\) est défini par l’expression

$$
c=a \cdot b \cdot \sin (\theta)
$$

où \(\theta\) est l’angle (le plus petit des deux) compris entre \(\vec{a}\) et \(\vec{b}\).

– La direction de \(\vec{c}\) est perpendiculaire au plan formé par \(\vec{a}\) et \(\vec{b}\). Son sens est défini par la règle de la main droite.

Calcul d’aires

\( \textbf{Proposition}\):

Soit \(\vec{a}\) et \(\vec{b}\) des vecteurs de l’espace.

L’aire \(\mathcal{A}\) du parallélogramme construit sur les vecteurs \(\vec{a}\) et \(\vec{b}\) est donnée par :

$$
\mathcal{A}=\|\vec{a} \times \vec{b}\|
$$

Preuve: Par ce qui précède, on a :

$$
\|\vec{a} \times \vec{b}\|=\|\vec{a}\| \cdot\|\vec{b}\| \cdot \sin (\theta)=\|\vec{a}\| \cdot h
$$

qui est égal à l’aire du parallélogramme construit sur \(\vec{a}\) et \(\vec{b}\).

Test de coplanarité

Test de coplanarité I: Trois vecteurs \(\vec{a}, \vec{b}\) et \(\vec{c}\) de l’espace sont coplanaires si et seulement \(\operatorname{si}(\vec{a} \times \vec{b}) \cdot \vec{c}=0\)

\( \textbf{Définition}\):

Relativement à une base \(\mathcal{B}\) de l’espace, on donne :

$$
\vec{a}=\left(\begin{array}{l}
a_{1} \\
a_{2} \\
a_{3}
\end{array}\right), \vec{b}=\left(\begin{array}{l}
b_{1} \\
b_{2} \\
b_{3}
\end{array}\right) \text { et } \vec{c}=\left(\begin{array}{c}
c_{1} \\
c_{2} \\
c_{3}
\end{array}\right)
$$

On appelle déterminant des vecteurs \(\vec{a}, \vec{b}\) et \(\vec{c}\), noté \(\operatorname{det}(\vec{a} ; \vec{b} ; \vec{c})\), le nombre défini par :

$$
\begin{aligned}
\operatorname{det}(\vec{a} ; \vec{b} ; \vec{c}) & =\left|\begin{array}{lll}
a_{1} & b_{1} & c_{1} \\
a_{2} & b_{2} & c_{2} \\
a_{3} & b_{3} & c_{3}
\end{array}\right|=a_{1}\left|\begin{array}{ll}
b_{2} & c_{2} \\
b_{3} & c_{3}
\end{array}\right|-a_{2}\left|\begin{array}{ll}
b_{1} & c_{1} \\
b_{3} & c_{3}
\end{array}\right|+a_{3}\left|\begin{array}{ll}
b_{1} & c_{1} \\
b_{2} & c_{2}
\end{array}\right| \\
& =a_{1}\left(b_{2} c_{3}-b_{3} c_{2}\right)-a_{2}\left(b_{1} c_{3}-b_{3} c_{1}\right)+a_{3}\left(b_{1} c_{2}-b_{2} c_{1}\right) \\
& =a_{1} b_{2} c_{3}-a_{1} b_{3} c_{2}-a_{2} b_{1} c_{3}+a_{2} b_{3} c_{1}+a_{3} b_{1} c_{2}-a_{3} b_{2} c_{1}
\end{aligned}
$$

\( \textbf{Proposition}\):

\(\operatorname{det}(\vec{a} ; \vec{b} ; \vec{c})=(\vec{a} \times \vec{b}) \cdot \vec{c}\)

Remarque: Pour désigner ce déterminant, on parle parfois de produit mixte, puisqu’il relie en une seule expression le produit scalaire et le produit vectoriel.

Test de coplanarité II: Trois vecteurs \(\vec{a}, \vec{b}\) et \(\vec{c}\) de l’espace sont coplanaires si et seulement si \(\operatorname{det}(\vec{a} ; \vec{b} ; \vec{c})=0\)

Calcul de volumes

\( \textbf{Proposition}\):

Soit \(\vec{a}, \vec{b}\) et \(\vec{c}\) des vecteurs de l’espace.

– Le volume \(\mathcal{V}_{\text {paral }}\) du parallélépipède construit sur les vecteurs \(\vec{a}, \vec{b}\) et \(\vec{c}\) est donné par :

$$
\mathcal{V}_{\text {paral }}=|\operatorname{det}(\vec{a} ; \vec{b} ; \vec{c})|
$$

– Le volume \(\mathcal{V}_{\text {tétra }}\) du tétraèdre construit sur les vecteurs \(\vec{a}, \vec{b}\) et \(\vec{c}\) est donné par :

$$
\mathcal{V}_{\text {tétra }}=\frac{1}{6}|\operatorname{det}(\vec{a} ; \vec{b} ; \vec{c})|
$$

Test de Coplanarité

Déterminant et Volume

Test de Colinéarité

Exercice

Exercice Calcul de la distance entre un point et une droite en utilisant le produit vectoriel